How to Find All Paths Between Two Nodes

To find all paths between two nodes, we will create a weighted directed graph and use depth-first search. Our graph will be able to find all paths between two nodes and sort the found paths by their cost. We will find all paths between two vertices with Depth First Search. We will save them so we can do something with the paths. The reason for this is that finding examples of finding all paths between two nodes are scarce, especially if you do not want to print them.

This article assumes you have some knowledge of what a graph is and how it works. You should know that in computer science, a graph is made up of vertices and edges. Let’s go through some of the terminologies we will use:

• Vertices are the plural form of a vertex (node), vertices are, therefore, a set of nodes.
• Edge is a pair (v,w) containing two vertices, which means they connect to each other.
• A directed graph is when an edge has a direction to another edge
• Weighted graph means that each edge has a cost or weight.
• A path is a sequence of adjacent vertices

Before we continue, let us set up an objective. We want to find all paths from A to F, the image shows how the graph looks like, and the cost of the edges.

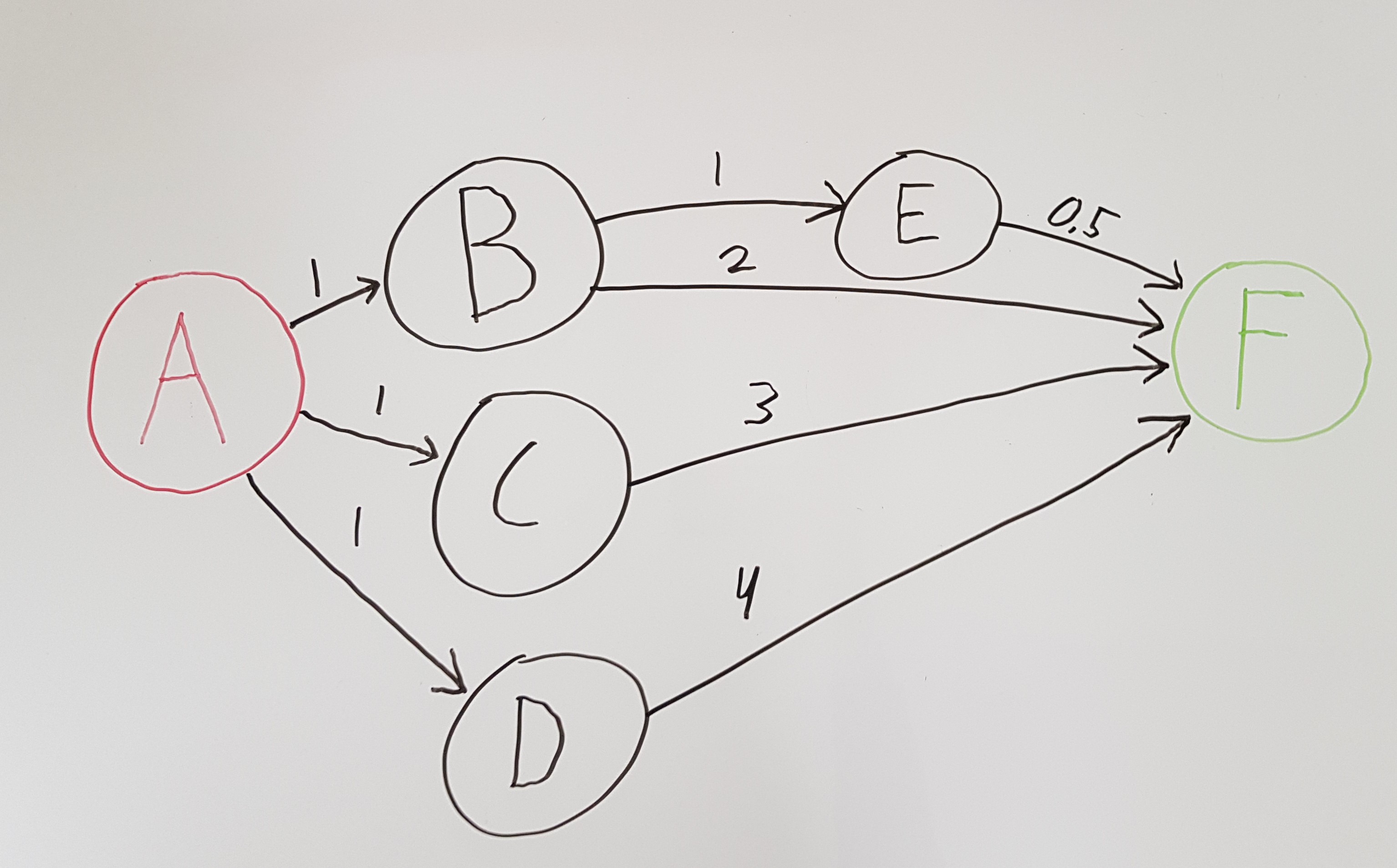
Your graph might not be this simplistic, but the solution will work for a more complex graph as well. We want the following result returned:

[
   {'path': ['A', 'B', 'E', 'F'], 'cost': 2.5},
   {'path': ['A', 'B', 'F'], 'cost': 3},
   {'path': ['A', 'C', 'F'], 'cost': 4},
   {'path': ['A', 'D', 'F'], 'cost': 5}
]

Depth First Search

We will use DFS (Depth First Search) to find all paths, as previously stated. But why do we use Depth First Search? To understand why let’s look at what DFS is and how it works.

We can use DFS to see if there exists a path between vertex x and vertex y. The starting vertex children are asked if they either are vertex y or if it’s a child of theirs. This goes on recursively until we actually find vertex y if we now do find it. The reason why we call it “depth-first search” is because it checks one child at a time, which means it traverses down a single path at a time, when it can’t traverse anymore it will backtrack. To ensure we do not revisit a vertex that we already have visited we will mark it as visited = true, this is really important because in graphs cycles may occur.

The Code

Enough planning, let us start coding. For demonstration purposes, we use Python.

Vertex class

Firstly we create our Vertex class. I’ve created this vertex, so it has a key, a value, and a currCost. I added key to allow duplicates of data (values). currCost is not the cost of an edge, but it is the entire cost of a path.

class Vertex:
   """The vertex used in the graph below"""
   def __init__(self, key, data):
       self.adjancencyList = {}
       self.key = key
       self.data = data
       self.currCost = 0  # stores own weight added with followers in path

   def connect(self, otherVertex, weight):
       self.adjancencyList[otherVertex] = weight

   def get_connections(self):
       return self.adjancencyList.keys()

   def get_cost(self, vertex):
       return self.adjancencyList[vertex]

Graph class

For the graph, I'll let the code speak for itself. I recommend studying the def dfs(self, currVertex, destVertex, visited, path, fullPath) method extra carefully since that's the most important part. In the last section, we will test the code together.

from Vertex import Vertex

"""
This class is a weighted directed graph that is
supposed to be able to find all paths between two nodes

* The graph sorts all the paths by weight
* The graphs vertices uses keys to allow duplicates of data
* The graphs depth first search is based on recursion
"""

class Graph:
   """graph used to find all paths between two nodes using DFS"""
   def __init__(self):
       self.numberOfVertices = 0
       self.vertices = {}

   def add(self, key, data):
       """adds a vertex to graph and saves vertex based on unique key"""
       if key not in self.vertices:
           self.numberOfVertices += 1
           self.vertices[key] = Vertex(key, data)
           return True

       return False

   def addEdge(self, fromVertex, toVertex, weight):
       """connects two vertices"""
       if fromVertex in self.vertices and toVertex in self.vertices:
           self.vertices[fromVertex].connect(toVertex, weight)
           return True

       return False

   def getAllPaths(self, start, end):
       return self.dfs(start, end, [], [], [])

   def getAllPathsSorted(self, start, end):
       res = self.dfs(start, end, [], [], [])
       return sorted(res, key=lambda k: k['cost'])

   def dfs(self, currVertex, destVertex, visited, path, fullPath):
       """finds all paths between two nodes, returns all paths with their respective cost"""

       # get vertex, it is now visited and should be added to path
       vertex = self.vertices[currVertex]
       visited.append(currVertex)
       path.append(vertex.data)

       # save current path if we found end
       if currVertex == destVertex:
           fullPath.append({"path": list(path), "cost": vertex.currCost})

       for i in vertex.get_connections():
           if i not in visited:
               self.vertices[i].currCost = vertex.get_cost(i) + vertex.currCost
               self.dfs(i, destVertex, visited, path, fullPath)

       # continue finding paths by popping path and visited to get accurate paths
       path.pop()
       visited.pop()

       if not path:
           return fullPath

The result

Let’s try out the Graph class and see if it returns all the paths by creating a unit test. We set up a graph like just like the image in the beginning.

import unittest
from Graph import Graph

class GraphTest(unittest.TestCase):

    def setUp(self):
        self.graph = Graph()

    def tearDown(self):
        self.graph = None

    # Should return all paths sorted by cost
    def test_FindAllPathsSorted(self):

        ## Add vertices
        self.graph.add("A", "A")
        self.graph.add("B", "B")
        self.graph.add("C", "C")
        self.graph.add("D", "D")
        self.graph.add("E", "E")
        self.graph.add("F", "F")

        # Add edges for path 1
        self.graph.addEdge("A", "B", 1)
        self.graph.addEdge("B", "E", 1)
        self.graph.addEdge("E", "F", 0.5)

        # Add edges for path 2
        self.graph.addEdge("B", "F", 2)

        # Add edges for path 3
        self.graph.addEdge("A", "C", 1)
        self.graph.addEdge("C", "F", 3)

        # Add edges for path 4
        self.graph.addEdge("A", "D", 1)
        self.graph.addEdge("D", "F", 4)

        # Get all the paths sorted
        res = self.graph.getAllPathsSorted("A", "F")
 
        self.assertEqual(res[0]["path"], ['A', 'B', 'E', 'F'])
        self.assertEqual(res[0]["cost"], 2.5)

        self.assertEqual(res[1]["path"], ['A', 'B', 'F'])
        self.assertEqual(res[2]["path"], ['A', 'C', 'F'])
        self.assertEqual(res[3]["path"], ['A', 'D', 'F'])

if __name__ == '__main__':
    unittest.main()

Let's run the test with python GraphTest.py

Ran 1 test in 0.000s

OK

You can do some pretty cool things with this. I assume you have something in mind since you read this article. Be aware, that depending on how many vertices you have this might take a long, long, long time.